BZOJ3527: [ZJOI2014] 力 - NekoMio's Blog

Description#

给出n个数qi，给出Fj的定义如下：
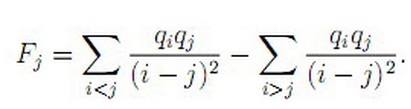
令Ei=Fi/qi，求Ei.

Input#

第一行一个整数n。
接下来n行每行输入一个数，第i行表示qi。
n≤100000，0<qi<1000000000

Output#

n行，第i行输出Ei。与标准答案误差不超过1e-2即可。

Sample Input#

1
5
2
4006373.885184
3
15375036.435759
4
1717456.469144
5
8514941.004912
6
1410681.345880

Sample Output#

1
-16838672.693
2
3439.793
3
7509018.566
4
4595686.886
5
10903040.872

题解#

写写题解证明自己还活着

这道题是一道比较基础的题目

先把Ei写出来得

$E_i = \sum_{i<j} {\frac{p_i}{(i - j) ^ 2}} - \sum_{i>j}{\frac{qi}{(i - j)^2}}$

令 $f(i) = q_i,\ g(i) = \frac{1}{i^2}$

$E_j=\sum_{i=1}^{j-1}f(i) \times g(j-i)-\sum_{i=j+1}^nf(i) \times g(j-i)$

前一部分直接FFT算。

后一部分 $\sum_{i=j+1}^nf(i) \times g(j-i)=\sum_{i=1}^{n-j}f(i+j) \times g(i)$

令 $f'(n-i-j)=f(i+j)$ ，则第二部分变为 $\sum_{i=0}^{n-j-1}f'(n-i-j-1) \times g(i)$ ，转化为卷积的形式用FFT解即可。

1
#include <cstdio>
2
#include <cstring>
3
#include <algorithm>
4
#include <cmath>
5
#include <complex>
6
using namespace std;
7
#define Complex complex<double>
8
const double pi = acos(-1.);
9
inline int read()
10
{
11
    int x=0,f=1;char ch=getchar();
12
    while (ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
13
    while (ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
14
    return x*f;
15
}
16
const int MAXN = 100005 * 8;
17
int rev[MAXN];
18
double Inv;
19
int N;
20
void FFt(Complex *a, int op)
21
{
22
    Complex t, w;
23
    for (int i = 0; i < N; i++)
24
        if (i > rev[i]) swap(a[i], a[rev[i]]);
25
    for (int k = 2; k <= N; k <<= 1)
26
    {
27
        Complex wn(cos(pi / (k >> 1)), op * sin(pi / (k >> 1)));
28
        for (int j = 0; j < N; j += k)
29
        {
30
            w = Complex(1, 0);
31
            for (int i = 0; i < (k >> 1); i++, w = w * wn)
32
            {
33
                t = a[i + j + (k >> 1)] * w;
34
                a[i + j + (k >> 1)] = a[i + j] - t;
35
                a[i + j] = a[i + j] + t;
36
            }
37
        }
38
    }
39
    if (op == -1)
40
        for (int i = 0; i < N; i++)
41
            a[i] *= Inv;
42
}
43
Complex a[MAXN], b[MAXN], g[MAXN];
44
int main()
45
{
46
    int n = read();
47
    n--;
48
    for (int i = 0; i <= n; i++)
49
    {
50
        double x;
51
        scanf ("%lf", &x);
52
        b[n - i] = a[i] = x;
53
    }
54
    for (int i = 1; i <= n; i++) g[i] = (1. / i / i);
55
    int m = n + n + 1;
56
    N = 1;
57
    while (N < m)
58
        N <<= 1;
59
    Inv = 1. / N;
60
    for (int i = 0; i < N; i++)
61
        if (i & 1)
62
            rev[i] = (rev[i >> 1] >> 1) | (N >> 1);
63
        else
64
            rev[i] = (rev[i >> 1] >> 1);
65
    FFt(a, 1), FFt(b, 1), FFt(g, 1);
66
    for (int i = 0; i < N; i++) a[i] = a[i] * g[i];
67
    for (int i = 0; i < N; i++) b[i] = b[i] * g[i];
68
    FFt(a, -1), FFt(b, -1);
69
    for (int i = 0; i <= n; i++)
70
        printf ("%.3f\n", a[i].real() - b[n - i].real());
71
    // while (1);
72
}