NOIP模拟超级树 - NekoMio's Blog

3.1 描述#

一棵k-超级树可按如下方法得到：取一棵深度为k的满二叉树，对每个节点，向它的所有祖先连边（如果这条边不存在的话）。例如，下图是一个4-超级树的例子：

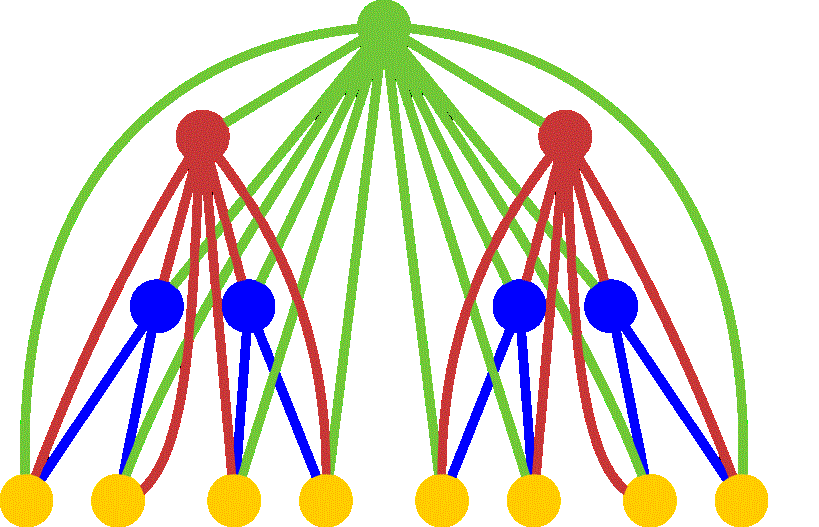现在你的任务是统计一棵k-超级树中有多少条每个节点最多经过一次的不同有向路径。两条路径被认为不同，当且仅当它们经过的节点的集合不同，或经过的节点的顺序不同。由于答案可能很大，请输出总路径数对mod取模后的结果。

3.2 输入#

一行两个整数k、mod，意义见上。

3.3 输出#

一行一个整数，代表答案

样例#

输入	输出
2 100	9
3 1000	245
20 998244353	450500168

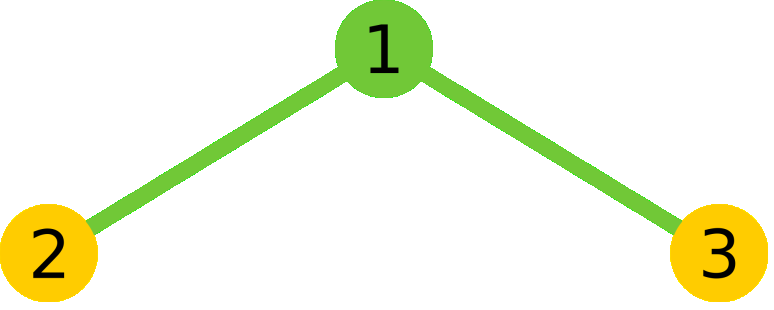
样例解释：对第一组样例，将节点如图编号，共有9条不同的路径：1, 2, 3, 1− 2, 2 − 1, 1 − 3, 3 − 1, 2 − 1 − 3, 3 − 1 − 2。

限制与约定#

对于10%的数据，k ≤ 4。对于40%的数据，k ≤ 10。对于60%的数据，k ≤ 100。另有10%的数据，mod = 998244353。对于所有数据，1 ≤ k ≤ 300，1 ≤ mod ≤ 109。

题解#

考虑dp[i][j]表示一棵i-超级树，有j条点不重复的路径的方案数。对于第二维表示有j条路径他们不相交的方案数这记num=dp[i][l]*dp[i][r]

1
dp[i+1][l+r]+=num
2
dp[i+1][l+r+1]+=num
3
dp[i+1][l+r]+=2*num*(l+r)
4
dp[i+1][l+r-1]+=2*num*l*r
5
dp[i+1][l+r-1]+=num*(l*(l-1)+r*(r-1))

dp[1][0]=dp[1][1]=1
答案为dp[k][1]

因为我们发现每次转移的时候j最多会减1
所以我们只需要前k-i+1个状态
只DP这些状态就可以了

1
#include <cstdio>
2
#include <cstring>
3
#include <algorithm>
4
using namespace std;
5
long long f[305][305];
6
int MOD;
7
int main()
8
{
9
  int k;
10
  scanf("%d%d", &k, &MOD);
11
  f[1][0] = f[1][1] = 1 % MOD;
12
  for (int i = 1; i < k; i++)
13
  {
14
    for (int l = 0; l <= k - i + 1; l++)
15
      for (int r = 0; r <= k - i + 1; r++)
16
      {
17
        long long num = f[i][l] * f[i][r] % MOD;
18
        if (r + l <= k - i)
19
        {
20
          f[i + 1][r + l] = (f[i + 1][r + l] + num) % MOD;
21
          f[i + 1][r + l] = (f[i + 1][r + l] + 2 * num * (l + r) % MOD) % MOD;
22
        }
23
        if (r + l + 1 <= k - i)
24
          f[i + 1][r + l + 1] = (f[i + 1][r + l + 1] + num) % MOD;
25
        if (r + l - 1 <= k - i)
26
        {
27
          f[i + 1][r + l - 1] = (f[i + 1][r + l - 1] + 2 * num * l * r % MOD) % MOD;
28
          f[i + 1][r + l - 1] = (f[i + 1][r + l - 1] + num * (l * (l - 1) + r * (r - 1)) % MOD) % MOD;
29
        }
30
      }
31
  }
32
  printf("%lld", f[k][1]);
33
}